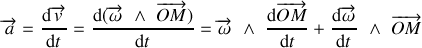La trajectoire du point est un cercle caractérisé par son centre
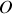 et son rayon
et son rayon
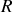 . Il est logique de choisir l'origine du repère en centre du cercle et l'axe
. Il est logique de choisir l'origine du repère en centre du cercle et l'axe
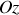 perpendiculaire au plan contenant la trajectoire. Le système de coordonnées polaires est bien adapté pour ce type de mouvement. Les équations horaires du mouvement peuvent s'écrire :
perpendiculaire au plan contenant la trajectoire. Le système de coordonnées polaires est bien adapté pour ce type de mouvement. Les équations horaires du mouvement peuvent s'écrire :
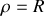 = constante et
= constante et
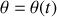 . La forme de la fonction
. La forme de la fonction
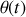 qualifiera le type de mouvement circulaire. Suivant la forme de la fonction
qualifiera le type de mouvement circulaire. Suivant la forme de la fonction
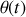 le mouvement sera dit circulaire et :
le mouvement sera dit circulaire et :
Uniforme si
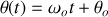 avec
avec
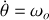 = constante
= constante
Uniformément varié (accéléré ou décéléré) si
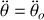 = constante soit
= constante soit
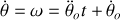 et
et
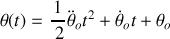
Sinusoïdale si
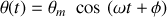
Mouvement circulaire quelconque
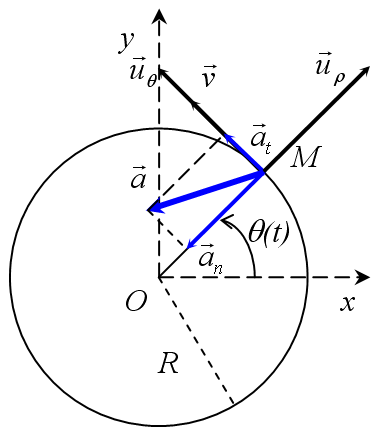
Les caractéristiques cinématiques du mouvement circulaire peuvent se déduire du schéma présenté sur la figure 15 et sont données par :
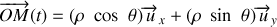
ou bien
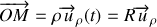
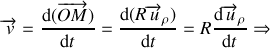
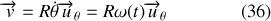
Ce résultat peut se retrouver en utilisant l'expression (19) de la vitesse en coordonnées polaires en posant
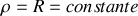 .
.
La dérivée du vecteur vitesse fait apparaître deux termes. On a :
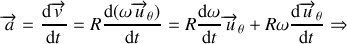
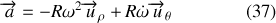
Remarque :
Le vecteur unitaire orthoradiale
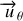 est perpendiculaire au rayon
est perpendiculaire au rayon
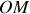 et est donc tangent à la trajectoire. Dans ce cas, en orientant la trajectoire dans le sens trigonométrique, il correspond au vecteur
et est donc tangent à la trajectoire. Dans ce cas, en orientant la trajectoire dans le sens trigonométrique, il correspond au vecteur
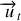 de la base de Frenet (voir II.7 base de Frenet). L'autre vecteur
de la base de Frenet (voir II.7 base de Frenet). L'autre vecteur
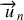 de cette base est toujours tourné vers la concavité et est opposé au vecteur
de cette base est toujours tourné vers la concavité et est opposé au vecteur
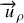 . On a donc :
. On a donc :
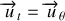 et
et
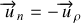
On retrouve l'expression de la valeur algébrique
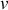 de la vitesse :
de la vitesse :
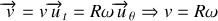
L'expression du vecteur accélération s'écrit dans la base de Frenet (voir équation 35)
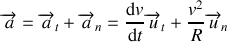
Composante radiale ou accélération normale
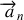
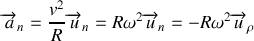
Le terme (
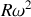 ) étant positif, on constate que cette accélération est toujours dirigée vers le centre du cercle : c'est la composante normale centripète. C'est elle « qui fait tourner » c'est-à-dire qui rend compte de la variation de la direction du vecteur vitesse. Même si le mouvement est uniforme (
) étant positif, on constate que cette accélération est toujours dirigée vers le centre du cercle : c'est la composante normale centripète. C'est elle « qui fait tourner » c'est-à-dire qui rend compte de la variation de la direction du vecteur vitesse. Même si le mouvement est uniforme (
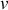 et
et
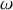 constantes) cette accélération existe nécessairement.
constantes) cette accélération existe nécessairement.
Composante orthoradiale ou tangentielle
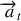
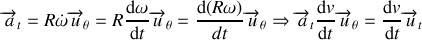
Cette accélération indique si la valeur de la vitesse varie ou pas. Dans le cas du mouvement circulaire uniforme il est nul. La figure 15 représente les vecteurs vitesse et accélération pour un mouvement circulaire quelconque. Dans le cas où l'accélération tangentielle est dirigée comme le vecteur vitesse le mouvement est accéléré. Dans le cas contraire le mouvement serait freiné.
Mouvement circulaire uniforme
Définition :
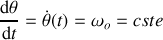 (l'équation différentielle du mouvement)
(l'équation différentielle du mouvement)
L'équation horaire
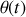 est obtenue par intégration. Avec, à l'instant initial
est obtenue par intégration. Avec, à l'instant initial
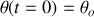 , on a :
, on a :
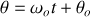
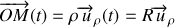
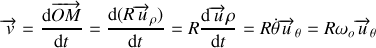
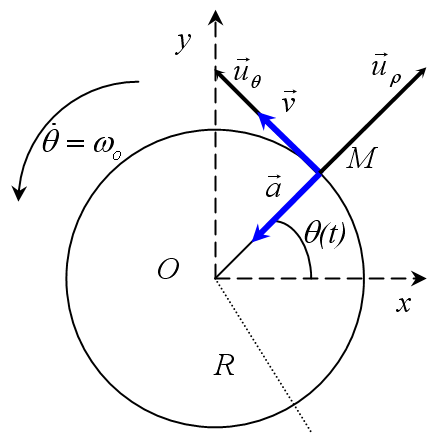
L'expression (37) du vecteur accélération se simplifie. La vitesse angulaire étant constante la composante tangentielle du vecteur accélération est nulle. Il ne reste que la composante normale :
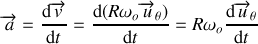
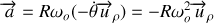
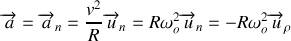
Remarque :
Le mouvement circulaire uniforme est un mouvement accéléré dont l'accélération est centripète. Uniforme ne veut donc pas dire accélération nulle.
La figure 16 représente les vecteur vitesse et accélération pour un mouvement circulaire uniforme.
Expressions générales des vecteurs vitesse et accélération pour un mouvement circulaire
Les vecteurs vitesse et accélération peuvent s'exprimer en introduisant le vecteur vitesse angulaire
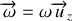 (voir expression 27). En utilisant la relation que
(voir expression 27). En utilisant la relation que
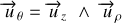 on obtient une expression du vecteur vitesse indépendante de la base choisie :
on obtient une expression du vecteur vitesse indépendante de la base choisie :
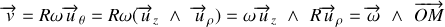
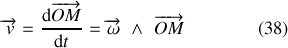
Le vecteur position
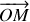 est un vecteur de norme constante (rayon
est un vecteur de norme constante (rayon
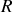 du cercle) qui tourne. La dérivée de ce vecteur (voir expression (30)) est un vecteur qui lui est directement perpendiculaire et dont la norme a été multipliée par la vitesse angulaire. L'expression (38) permet d'exprimer cette dérivée indépendamment de la base choisie.
du cercle) qui tourne. La dérivée de ce vecteur (voir expression (30)) est un vecteur qui lui est directement perpendiculaire et dont la norme a été multipliée par la vitesse angulaire. L'expression (38) permet d'exprimer cette dérivée indépendamment de la base choisie.
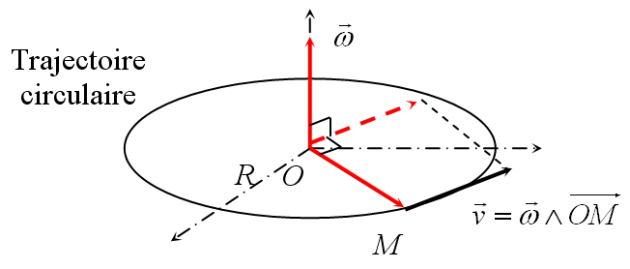
Figure 17 : Lien entre vecteur vitesse
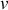 et vecteur vitesse angulaire
et vecteur vitesse angulaire
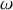
Cette relation est valable pour tout mouvement circulaire. La même règle peut être utilisée pour déterminer le vecteur accélération :
Composante radiale :
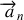
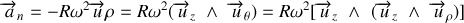
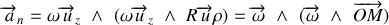
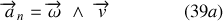
En utilisant la relation (38) on peut encore écrire :
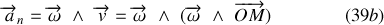
Composante orthoradiale
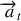 :
:
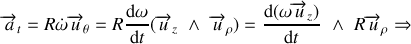
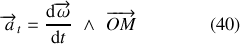
Le vecteur accélération
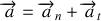
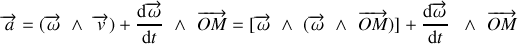
Ce résultat peut être obtenu directement en dérivant le vecteur vitesse exprimé sous forme d'un produit vectoriel et en appliquant la règle habituelle de dérivation d'un produit de fonction :